Funcție de stare și spațiu Hilbert
În mecanica cuantică o stare dinamică a unui sistem atomic este descrisă cantitativ de o funcție de stare (numită, într-o formulare particulară, funcție de undă). Comportarea ondulatorie a sistemelor atomice arată că stările lor ascultă de principiul superpoziției; pe plan teoretic, aceasta înseamnă că funcțiile de stare sunt elemente ale unui spațiu vectorial.Pentru interpretarea fizică a funcției de stare e necesar ca vectorii din spațiul stărilor să poată fi caracterizați prin orientare și mărime. Acest lucru se realizează definind un produs scalar, ceea ce transformă spațiul stărilor într-un spațiu prehilbertian. Produsul scalar a doi vectori
 și
și  este un număr complex
este un număr complex  cu proprietățile
cu proprietățile
În general, spațiul stărilor este infinit-dimensional; pentru a putea cuprinde în totalitate stările sistemului, se impune condiția ca el să fie complet, ceea ce îl face să devină un spațiu Hilbert.
Observabile și operatori hermitici
Starea unui sistem, la un anumit moment, este caracterizată prin valorile măsurate, în acel moment, ale unui număr de mărimi fizice observabile. Analiza operației de măsurare arată că măsurarea unei observabile modifică starea sistemului, iar măsurarea simultană (adică în succesiune imediată) a două observabile poate da rezultate diferite, în funcție de ordinea în care au fost efectuate măsurătorile. Teoria incorporează aceste constatări atașând fiecărei dintre observabilele ale sistemului un operator liniar
ale sistemului un operator liniar  în spațiul Hilbert, operației de măsurare a observabilei
corespunzându-i aplicarea operatorului reprezentativ asupra funcției de
stare. Algebra acestor operatori este necomutativă, adică în general
în spațiul Hilbert, operației de măsurare a observabilei
corespunzându-i aplicarea operatorului reprezentativ asupra funcției de
stare. Algebra acestor operatori este necomutativă, adică în general  comutatorul a doi operatori
comutatorul a doi operatori  și
și  notat
notat ![\, \left[ A , B \right] \, ,](http://upload.wikimedia.org/math/0/9/3/093334fb01a76ddc8322b897d6911d21.png) este operatorul
este operatorul și
și  se numesc compatibile dacă operatorii atașați comută (comutatorul lor este nul).[2]
se numesc compatibile dacă operatorii atașați comută (comutatorul lor este nul).[2]Valori proprii și vectori proprii
Se mai face ipoteza că valoarea rezultată din măsurarea unei observabile este una dintre valorile proprii ale operatorului atașat, iar starea sistemului imediat după efectuarea măsuratorii este un vector propriu corespunzător acestei valori; întrucât observabilele au valori reale, operatorii reprezentativi trebuie să fie operatori hermitici. Un operator liniar este un operator hermitic dacă pentru orice pereche de vectori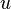 și
și  din spațiul Hilbert are loc relația
din spațiul Hilbert are loc relația este o constantă, are soluții nebanale (adică diferite de vectorul nul)
doar pentru anumite valori ale acestei constante, numite valori proprii
ale operatorului
este o constantă, are soluții nebanale (adică diferite de vectorul nul)
doar pentru anumite valori ale acestei constante, numite valori proprii
ale operatorului 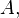 iar soluțiile corespunzătoare se numesc vectori proprii.
iar soluțiile corespunzătoare se numesc vectori proprii.Din relațiile (1) și (4) rezultă că într-adevăr valorile proprii ale unui operator hermitic sunt numere reale; mulțimea tuturor valorilor proprii constituie spectrul operatorului. Spectrul este în general discret, adică o mulțime numărabilă, ale cărei elemente pot fi indexate printr-un număr întreg, în forma
 Vectorii proprii corespunzători unor valori proprii diferite sunt ortogonali: dacă
Vectorii proprii corespunzători unor valori proprii diferite sunt ortogonali: dacă  și
și 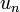 sunt vectori proprii corespunzători, respectiv, valorilor proprii
sunt vectori proprii corespunzători, respectiv, valorilor proprii  atunci
atunci  Unei valori proprii îi pot corespunde mai mulți vectori proprii liniar independenți, în care caz ea se zice degenerată, iar numărul maxim de vectori proprii liniar independenți care îi corespunde este ordinul de degenerare; fenomenul se numește degenerescență. Acești vectori nu sunt, în general, ortogonali, însă există metode de ortogonalizare
prin care se poate construi, în subspațiul invariant asociat unei
valori proprii degenerate, un sistem echivalent de vectori ortogonali.
Împărțind fiecare vector propriu prin norma sa, se obține un sistem ortonormat complet de vectori proprii, caracterizat prin
Unei valori proprii îi pot corespunde mai mulți vectori proprii liniar independenți, în care caz ea se zice degenerată, iar numărul maxim de vectori proprii liniar independenți care îi corespunde este ordinul de degenerare; fenomenul se numește degenerescență. Acești vectori nu sunt, în general, ortogonali, însă există metode de ortogonalizare
prin care se poate construi, în subspațiul invariant asociat unei
valori proprii degenerate, un sistem echivalent de vectori ortogonali.
Împărțind fiecare vector propriu prin norma sa, se obține un sistem ortonormat complet de vectori proprii, caracterizat prin e simbolul Kronecker (care are valoarea 1 pentru indici egali și 0 pentru indici diferiți).
e simbolul Kronecker (care are valoarea 1 pentru indici egali și 0 pentru indici diferiți).Dacă două observabile
 și
și  comută, ele admit (cel puțin) un sistem ortonormat complet comun de vectori proprii — și reciproc.[3] În prezența degenerescenței, acest sistem nu este, în general, unic. Se poate însă găsi un ansamblu de observabile
comută, ele admit (cel puțin) un sistem ortonormat complet comun de vectori proprii — și reciproc.[3] În prezența degenerescenței, acest sistem nu este, în general, unic. Se poate însă găsi un ansamblu de observabile  care comută două câte două și admit un sistem ortonormat complet unic de vectori proprii; este ceea ce se numeste un sistem complet de observabile care comută.
care comută două câte două și admit un sistem ortonormat complet unic de vectori proprii; este ceea ce se numeste un sistem complet de observabile care comută.Reprezentări
Mulțimea vectorilor proprii ai unui operator hermitic atașat unei observabile
atașat unei observabile  formează un sistem complet în spațiul Hilbert; orice vector de stare poate fi descompus în mod unic în această bază, presupusă ortonormată conform relației (6), în forma
formează un sistem complet în spațiul Hilbert; orice vector de stare poate fi descompus în mod unic în această bază, presupusă ortonormată conform relației (6), în forma atașat unei observabile
atașat unei observabile  asupra bazei ortonormate alese pot fi descompuse la rândul lor conform (7):
asupra bazei ortonormate alese pot fi descompuse la rândul lor conform (7):
Baza ortonormată de vectori proprii ai operatorului
 definește reprezentarea observabilei
definește reprezentarea observabilei  în care vectorilor de stare le corespund matrici coloană
în care vectorilor de stare le corespund matrici coloană  iar operatorilor matrici pătrate
iar operatorilor matrici pătrate  În reprezentarea proprie, matricea unui operator este diagonală și are drept elemente diagonale valorile proprii
În reprezentarea proprie, matricea unui operator este diagonală și are drept elemente diagonale valorile proprii  Trecerea de la o reprezentare la alta se realizează printr-o transformare unitară în spațiul Hilbert.
Trecerea de la o reprezentare la alta se realizează printr-o transformare unitară în spațiul Hilbert.Spectru continuu
În situații foarte idealizate (de exemplu în cazul particulei libere să se miște în întreg spațiul), spectrul (sau numai o parte a spectrului) poate deveni continuu; pentru vectorii proprii corespunzători nu se poate defini o normă. Dificultatea se ocolește prin normarea la funcția delta[4], în loc de simbolul Kronecker. Cu această convenție, relațiile (6) și (7) devin, în cazul spectrului continuu[5],Dinamică și hamiltoniană
Evoluția temporală a sistemului sub acțiunea forțelor existente (dinamica sistemului) trebuie să respecte principiul cauzalității, care cere ca starea sa la un anumit moment să determine în mod univoc starea sa la un moment ulterior. Modificarea funcției de stare și a oricărui operator hermitic
și a oricărui operator hermitic  care reprezintă o mărime observabilă, de la un moment inițial
care reprezintă o mărime observabilă, de la un moment inițial 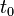 la un moment
la un moment  poate fi descrisă de un operator
poate fi descrisă de un operator  care trebuie să fie liniar și unitar (pentru ca evoluția temporală să păstreze superpoziția stărilor și spectrul observabilelor):
care trebuie să fie liniar și unitar (pentru ca evoluția temporală să păstreze superpoziția stărilor și spectrul observabilelor): care determină dinamica, se numește hamiltoniana sistemului. Efectele cuantice sunt introduse în teorie de constanta universală
care determină dinamica, se numește hamiltoniana sistemului. Efectele cuantice sunt introduse în teorie de constanta universală  numită constanta Planck redusă, care are dimensiunile unei acțiuni (energie
numită constanta Planck redusă, care are dimensiunile unei acțiuni (energie  timp).
timp).Formularea Schrödinger
În formularea dată de Schrödinger mecanicii cuantice (mecanică ondulatorie), operatorii hermitici asociați observabilelor nu depind de timp. Funcția de stare, numită funcție de undă, evoluează conform ecuației lui Schrödinger
asociați observabilelor nu depind de timp. Funcția de stare, numită funcție de undă, evoluează conform ecuației lui SchrödingerDacă hamiltoniana nu depinde de timp, ea este operatorul asociat observabilei energie. Ecuația (18) se integrează în forma
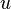 satisface ecuația lui Schrödinger independentă de timp
satisface ecuația lui Schrödinger independentă de timp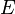 (stare staționară).
(stare staționară).Formularea Heisenberg
Aplicând funcției de undă și operatorilor independenți de timp
și operatorilor independenți de timp  din formularea Schrödinger transformarea unitară dependentă de timp
din formularea Schrödinger transformarea unitară dependentă de timp  rezultatul va fi o funcție de stare independentă de timp și operatori dependenți de timp care satisfac ecuația lui Heisenberg
rezultatul va fi o funcție de stare independentă de timp și operatori dependenți de timp care satisfac ecuația lui Heisenberg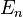 (valorile posibile ale energiei), ecuația precedentă are soluția
(valorile posibile ale energiei), ecuația precedentă are soluția comută cu hamiltoniana, observabila respectivă este o constantă a mișcării.
comută cu hamiltoniana, observabila respectivă este o constantă a mișcării.Formularea de interacție
Există formulări intermediare între cele două extreme Schrödinger și Heisenberg. Ele corespund împărțirii hamiltonienei în doi termeni a funcțiilor de stare și operatorilor care realizează trecerea de la formularea Schrödinger pentru
a funcțiilor de stare și operatorilor care realizează trecerea de la formularea Schrödinger pentru 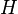 la formularea Heisenberg pentru
la formularea Heisenberg pentru  Funcția de stare va satisface ecuația lui Schrödinger cu hamiltoniana
Funcția de stare va satisface ecuația lui Schrödinger cu hamiltoniana 

 este hamiltoniana „liberă” a unui sistem pentru care soluția ecuației (25) este cunoscută exact, iar
este hamiltoniana „liberă” a unui sistem pentru care soluția ecuației (25) este cunoscută exact, iar  reprezintă o „interacție” pentru care soluția aproximativă a ecuației (24) este căutată prin metode perturbative.
reprezintă o „interacție” pentru care soluția aproximativă a ecuației (24) este căutată prin metode perturbative.Interpretare statistică
Articol principal: Operator statistic.
În interpretarea de la Copenhaga, se postulează că starea unui sistem atomic este descrisă complet de funcția de stare în spațiul Hilbert, iar această descriere este de natură statistică. Ea nu se referă la un exemplar izolat al sistemului, ci la un colectiv statistic
alcătuit dintr-un număr mare de exemplare „preparate” în aceeași stare
la un moment inițial și lăsate să evolueze neperturbate, conform
dinamicii conținute în hamiltoniană. Postulatele interpretarii
statistice se referă la rezultatele măsurării unei mărimi fizice
(observabile), efectuată pe fiecare dintre exemplarele colectivului
statistic la un moment ulterior. Măsurarea este presupusă ideală,
în sensul că rezultatele ei reflectă numai fenomene cuantice
incontrolabile, nu și efecte datorate condițiilor de măsurare, care sunt
controlabile și pot fi compensate.[7] Funcția de stare  se presupune normată la unitate:[8]
se presupune normată la unitate:[8]Principiul cuantificării
Rezultatul măsurării mărimii fizice poate fi numai una din valorile proprii
poate fi numai una din valorile proprii  ale operatorului hermitic asociat
ale operatorului hermitic asociat 
Principiul descompunerii spectrale
Probabilitatea de a obține ca rezultat al măsurării valoarea din spectrul operatorului hermitic asociat
din spectrul operatorului hermitic asociat  este pătratul normei proiecției funcției de stare pe subspațiul acelei valori proprii.
este pătratul normei proiecției funcției de stare pe subspațiul acelei valori proprii.Introducând un indice suplimentar care să distingă între vectorii bazei ortonormate în spațiul Hilbert, corespunzători unei valori proprii
 degenerată de ordin
degenerată de ordin  și ținând seama de normarea funcției de stare (26), descompunerea spectrală (7) și relația de completitudine (9) iau respectiv formele[9]
și ținând seama de normarea funcției de stare (26), descompunerea spectrală (7) și relația de completitudine (9) iau respectiv formele[9] este atunci
este atunci Cunoscând probabilitățile, se poate calcula valoarea medie a observabilei:
Cunoscând probabilitățile, se poate calcula valoarea medie a observabilei:Valoarea medie a unei mărimi fizice
 reprezentată prin operatorul hermitic
reprezentată prin operatorul hermitic  pe colectivul statistic descris de funcția de stare
pe colectivul statistic descris de funcția de stare  este
estePrincipiul reducerii funcției de stare
Dacă rezultatul măsurării mărimii fizice este valoarea proprie
este valoarea proprie  funcția de stare după măsurare se află în subspațiul invariant asociat acestei valori proprii.
funcția de stare după măsurare se află în subspațiul invariant asociat acestei valori proprii.Reducerea funcției de stare[10] reprezintă efectul cuantic, incontrolabil experimental, care definește o măsurătoare ideală; funcția de stare după măsurătoare se referă la un colectiv statistic în general diferit de cel dinaintea măsurătorii. Dacă rezultatul măsurătorii este o valoare proprie degenerată, ea nu va determina univoc funcția de stare și colectivul statistic asociat: în acest caz măsurătoarea este incompletă. Pentru a caracteriza complet starea sistemului, este necesară măsurarea simultană a unui sistem complet de observabile care comută
 funcția de stare va fi vectorul propriu comun unic, corespunzător valorilor proprii măsurate
funcția de stare va fi vectorul propriu comun unic, corespunzător valorilor proprii măsurate  Sistemul atomic este astfel „preparat” pentru o nouă măsurătoare (completă sau incompletă) a stării sale la un moment ulterior.[11]
Sistemul atomic este astfel „preparat” pentru o nouă măsurătoare (completă sau incompletă) a stării sale la un moment ulterior.[11]Algebra observabilelor: relații de comutare
Principiile mecanicii cuantice nu specifică forma operatorilor hermitici care reprezintă mărimi fizice observabile, sau relațiile de comutare pe care ei le satisfac. Acestea se stabilesc, pentru sisteme simple care au un analog în mecanica clasică[12] sau în teoria cuantică veche, prin metode euristice în care intuiția are un rol. Rezultatele sunt apoi extinse la sisteme complexe, generalizate și abstractizate.[13]Poziție și impuls
Poziția unei particule materiale este indicată prin componentele carteziene ale vectorului de poziție este operatorul gradient (nabla). Rezultă relațiile de comutare
este operatorul gradient (nabla). Rezultă relațiile de comutareMoment cinetic
Definiția momentului cinetic orbital este preluată din mecanica clasică, având în vedere că în dezvoltarea produselor de operatori ordinea factorilor trebuie păstrată:Energie și hamiltoniană
Hamiltoniana clasică pentru o particulă de masă aflată sub acțiunea unor forțe care derivă dintr-un potențial este suma energiei cinetice și a energiei potențiale:
aflată sub acțiunea unor forțe care derivă dintr-un potențial este suma energiei cinetice și a energiei potențiale: aflată într-un câmp electromagnetic care derivă din potențialul vector
aflată într-un câmp electromagnetic care derivă din potențialul vector  și potențialul scalar
și potențialul scalar  relația precedentă devine
relația precedentă devine e viteza luminii în vid.
e viteza luminii în vid.În mecanica cuantică, hamiltoniana este operatorul de evoluție; dacă nu depinde explicit de timp, ea este operatorul atașat observabilei energie. Expresia sa e, formal, cea din mecanica clasică, ținând seama că mărimile dinamice
 e operatorul laplacian.
e operatorul laplacian.Se constată că ecuațiile lui Heisenberg (21) pentru operatorii poziție și impuls au aceeași formă ca ecuațiile canonice din mecanica hamiltoniană, dacă parantezele Poisson sunt înlocuite prin comutatorii respectivi, împărțiți la constanta
 [14] Această manifestare a principiului de corespondență sugerează următoarea generalizare a relațiilor (34), (36) și (37) la sisteme alcătuite din mai multe particule:
[14] Această manifestare a principiului de corespondență sugerează următoarea generalizare a relațiilor (34), (36) și (37) la sisteme alcătuite din mai multe particule: și
și  sunt, respectiv, componentele carteziene ale pozițiilor și impulsurilor
particulelor. Operatorul hamiltonian se obține din hamiltoniana clasică
sunt, respectiv, componentele carteziene ale pozițiilor și impulsurilor
particulelor. Operatorul hamiltonian se obține din hamiltoniana clasică
 înlocuind variabilele canonice prin operatorii respectivi — cu
precizarea că produsele de operatori necomutativi trebuie simetrizate.[15]
înlocuind variabilele canonice prin operatorii respectivi — cu
precizarea că produsele de operatori necomutativi trebuie simetrizate.[15]


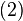


![\left[ A , B \right] = AB - BA \, .](http://upload.wikimedia.org/math/a/4/b/a4b2bb3e7ae22249125d168e7243b2a9.png)














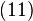



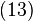



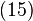









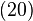

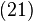
![i \hbar \frac{dA}{dt} = \left[ A , H \right] \, .](http://upload.wikimedia.org/math/f/0/6/f063f3563d986164fabf05d7d6589572.png)




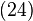


![i \hbar \frac{dA}{dt} = \left[ A , H^{(0)} \right] \, .](http://upload.wikimedia.org/math/5/1/b/51bcdf58dea7200047f4332c6189d7e6.png)










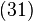

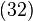




![[x, y] = 0 \, , \, [y, z ] = 0 \, , \, [z, x] = 0 \, .](http://upload.wikimedia.org/math/c/f/0/cf06c341d7cafa73ab404d369c334f90.png)


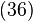
![[p_x, p_y] = 0 \, , \, [p_y, p_z ] = 0 \, , \, [p_z, p_x] = 0](http://upload.wikimedia.org/math/0/c/7/0c7b8b5c7535fc4275f9d21b113becae.png)

![[x, p_x] = i \hbar \, , \, [y, p_z ] = i \hbar \, , \, [z, p_x] = i \hbar \, ;](http://upload.wikimedia.org/math/5/b/e/5be691f852ef417f3d66131b72f92d29.png)



![[L_x, L_y] = i \hbar L_z \, , \, [L_y, L_z] = i \hbar L_x \, , \, [L_z, L_x] = i \hbar L_y \, .](http://upload.wikimedia.org/math/7/3/1/7317166407cb1b792b25a4d3a10c9acc.png)



![[\mathbf{L}^2 , L_x] = 0 \, , \, [\mathbf{L}^2 , L_y] = 0 \, , \, [\mathbf{L}^2 , L_z] = 0 \, .](http://upload.wikimedia.org/math/8/6/4/864a6b34e3083bf6ff2724888cc4d2db.png)







![[x_i,x_j] = 0 \, , \,[p_i,p_j] = 0 \, , \,[x_i,p_j] = i \hbar \delta_{ij} \, ,](http://upload.wikimedia.org/math/a/5/6/a563e3b75137206af33e86b5e22b2275.png)